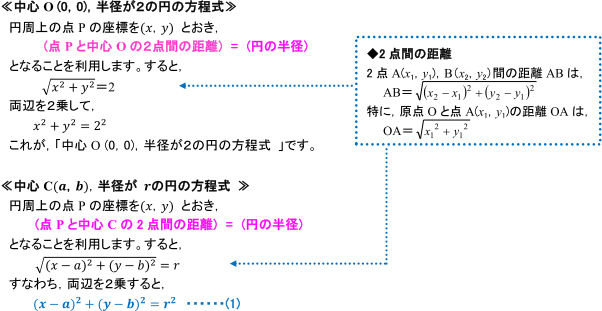
円の中心、半径の求め方 中心の座標と半径を求めるためには、円の方程式を次の形に変形する必要があります。 こうすることで、中心と半径を読み取ることができます。 というわけで、円の方程式を変形していきます。 まずは、並べかえて と をまとめ 3点を通る円POINT 円の通る3点から中心・半径を求める一般式を導出する. 計算フォーム・Excelにコピペして使えるフォーマットもあります. 単純な「連立方程式」の問題ですが,一般解は少し複雑な形になります. 計算フォーム Excel用フォーマット 導出 円の方程式 円の中心 円の 円錐の体積の求め方がわかる3つのステップ つぎの例題をときながらみていこう! Step1 円錐の「底面積」を計算するっ! まずは円錐の底面積を計算してみよう。 円錐の底面は「円」になっているね。 ってことは、 円の面積の公式 をつかって
2
エルボ 曲率 半径 求め 方
エルボ 曲率 半径 求め 方- まず、原点 O を中心とする 半径 r の円 と、その円上の 点 A ( x, y) を考えます。 「 x 軸の正の部分」と線分 O A による(反時計回りを正とする)角の大きさ ∠ B O A = θ に対して sin θ = y r , cos θ = x r , tan θ = y x で表される3つの三角比の関数のことを、 三角関数 と言います。 「 sin θ, cos θ, tan θ の分母・分子をド忘れしそう」と感じる方も多いかもしれませんが、これらはその サンシゴ (三・四・五)と言って、ロープひとつで直角を出すのに使ったりしますよね。 l = 180 length d = 10 depth r = (10² 180²)/ = (100 )/ = / = 1625 (検算) 1625² = ()² 180² = 1615² 180² = = 実際には、1/10にして計算するほうが楽です。 L=36、d=1、r=1625 とてつもなく大きな円になりますね。 (背景) ちな



円の面積の求め方を教えてください 4分の1の大きさの円 です Yahoo 知恵袋
円周の長さを求める公式は、次の通りです。 l = πd = 2πr l = π d = 2 π r 直径d、半径 r の円 ここで、l は円周の長さ、π は円周率、d は円の直径、r は円の半径を表します。 小学生向けに、文字を使わずに書くと次のようになります。 (円周)= (直径)×(円周率)= 2×(半径)×(円周率) 円周を求めるには、この公式に円の直径 d または 円の半径 r を代入すればよいです。 このページの続きでは、面積がπ㎝²、中心角が40°であるおうぎ形の半径を求めなさい。 今度は面積が与えられているので おうぎ形の面積の公式に当てはめていきましょう。 すると、このような方程式ができあがります。 これを解いていきましょう! 両辺をπで割って消し 正確には 2 × 2 × π = 4 π 例題②半径 5 cmの円の面積を求めて下さい。 答え: 5 × 5 × 314 = 785 (cm 2) 正確には 5 × 5 × π = 25 π ※円周率 π については「 円周の求め方・円周率とは何か・なぜ無限に続くのかを説明。 その割り切れない理由について 」の記事でくわしく解説しています。 ただ、この公式。 「半径 × 半径 × 314」が何をどう計算しているのか 具体的にイメージしにくい
星の表面積は半径 の二乗に比例します。 (球状の星を仮定しています) 星の光度は次の式で与えられます。 L = 4 p R 2 s T 4, Lは光度で、単位はワット、Rは半径で単位はメートル、 s はステファン・ボルツマン定数(567*10 8 Wm 2 K 4 ) Tは星の表面温度での収束半径をy のべき級数として求めてやってあとでxに変換する方向で考えましょう。 y のべき級数としてのn 次の項の係数をa n と書けば Ø Ø Ø Ø a n a n1 Ø Ø Ø Ø = 2n3 2n1 = 3 n 2 1 n → 1 ですから、y の級数として収束半径は1です。従ってxの級数としてもなお、シュヴァルツシルトは、シュワルツシルト半径を曲率が無限大になる半径として求めたが、実際にはこれは座標の取り方による一種のメトリックであり、曲率が無限大になるのは r = 0 の特異点で
これは大事な公式ですからしっかりと覚えておきましょう。 円の面積の求め方は、 (円の面積) = (半径) × (半径) × (円周率π) ですね。 ここまでわかれば、準備完了です。 ・底面の円の面積は 3×3×π=9π㎡ ・高さは 8cm よって、求める円柱のスペクトル半径 数学 における スペクトル半径 (スペクトルはんけい、 英 spectral radius )とは、複素正方 行列 や 線形位相空間 上の有界線形作用素の 固有値 の 絶対値 の 最小上界 のことである。 ギリシャ文字 ρ によって表記されることが多い。内接円の半径の計算方法 内接円 とは,三角形の3つの辺全てに接する円のこと。 内接円の半径は, S=\dfrac {r} {2} (abc) S = 2r(a b c) という公式を使って計算できる。 三角形の内接円について解説します。 前半では,内接円の半径を計算する方法を解説し
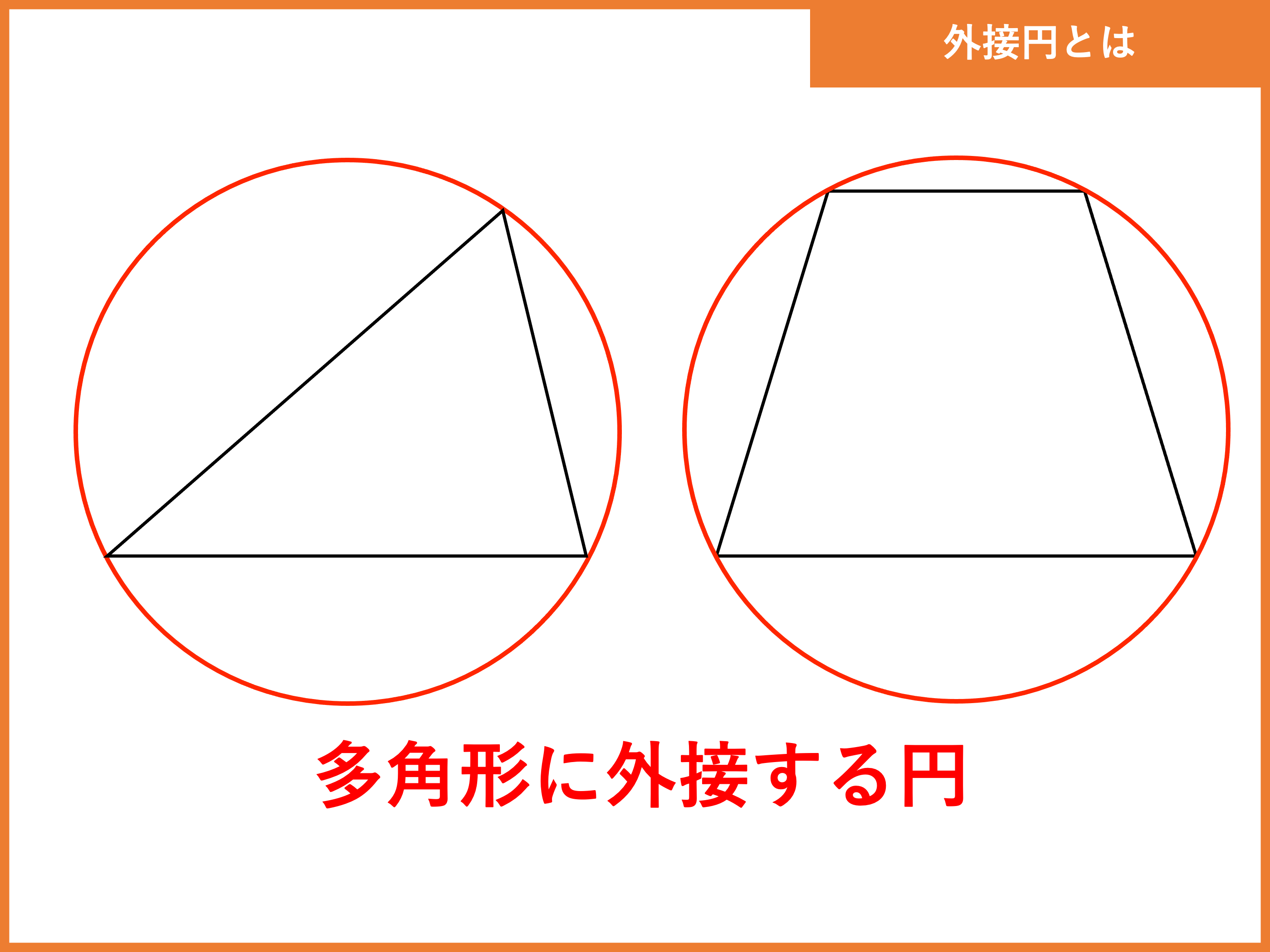



外接円とは 半径の公式や求め方 性質をわかりやすく解説 受験辞典




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ
電卓の使い方 面積を求める円の半径を入力して「計算」ボタンを押してください。 円周率は変更できます。 円周率で「πを使う」にチェックを入れると円周率をπとして計算します。 面積を入力して「計算」ボタンを押すと円の半径が計算されます送信を完了しました。 円の面積から半径 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学院生 主婦 会社員・公務員 自営業 エンジニア 教師・研究員 その他 この計算式は 非常に 最後に、外径と内径より管厚を求めていきます。 自分が今まで経験・勉強してきた「エクセル」「ビジネス用語」「生き方」などの情報を、なるべくわかりやすく、楽しく、発信していきます。 一緒に人生を楽しんでいきましょう



2




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
円の公式 円周・面積 円周率 = 3.14 円周の長さ = 直径 × 円周率 円周率 = 円周 ÷ 直径 おうぎ形の弧の長さ= 直径 × 314 × 中心角 ÷ 360 円の面積 = 半径 × 半径 × 円周率 円周の長さ 重要 円周率とは、「直径」を何倍したら「円周の長さ」になるかを表す数字です。 扇形の面積 求めたい半径の大きさを ㎝とすると 半径が ㎝で中心角が1°の扇形の面積は と、表すことができます。 そして、面積が ㎠になるはずだから という二次方程式が完成します。 あとは、これを解いていけば の値(半径)を求めることができ 弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン




円周 円の面積の求め方 チーム エン



半径の測定 測量
収束半径について べき級数が収束するか発散するかにはしきい値が存在します。このしきい値が収束半径です。複素数平面で考えると「半径」の意味が分かります。 ( 0 0 0 以外の)全ての z z z に対して発散するようなべき級数の収束半径は 0 0 0 です。 S 2- は16個,Cl - は17個,K は19個,Ca 2 は個の陽子を含んでおり、 陽子数が多いほど周りの電子を"グッ"と引き付けイオン半径は小さくなります 。 よって、 イオンの大きさは、S2- > Cl- > K > Ca2 となります。 参考・発展 今までの解説から、O 2- > F - > Ne > Na > Mg 2 > Al 3 であったり、S 2- > Cl - > Ar > K > Ca 2 となるのではないかと予想する人も半径rの求め方 半径rは、下式で求めます。 r=d/2 φと直径の関係は?1分でわかる意味、読み方、表記、外径、使い方 半径とr、直径、d、φとの違い 半径、直径、r、d、φとの違いを下記に整理しました。 半径 ⇒ 直径の半分の値



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




円の面積 算数用語集
曲率と曲率半径 例題 (1) 円の曲率 a a の円の曲率を求めよ。 答えは定義から簡単に出せます。 \rho = a ρ = a 。 したがって、曲率は である。 という風に即答のところですが、地味に習ったことを駆使して「計算」してみて、本当にそうなるかみておき 内接円の半径の求め方 三角形の内接円の半径を求める方法 については、学校の授業でもあまり強調して説明されません。 内接円の半径を直接求める公式があるのですが、覚えづらい形をしているので、丸暗記するのは危険です。 半径を求めるためには,中心の座標が分からないとどうにもなりません. そこで,とりあえず中心Rの座標を (x0, y0)とします. で,P1, P2, P3はRを中心とする円上にあるので, RとP1との距離,RとP2との距離,RとP3との距離は全て等しいはずで,しかもこれは円の半径です. そこで,とりあえず半径をrとします. これで材料はそろいました. 後は,連立方程式を解けばよいの




File 面心立方格子の原子半径の求め方 Svg Wikimedia Commons
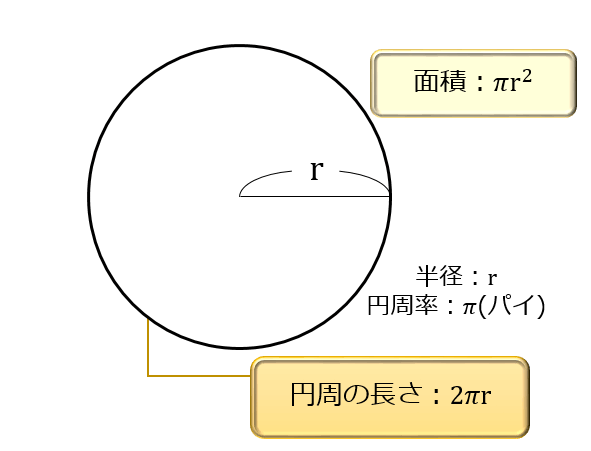



円周の求め方 円周率とは何か なぜ無限に続くのかを説明 その割り切れない理由について アタリマエ
ただし,すべての z \ne a z = a で発散するとき,収束半径は r= 0 r = 0 と定め,すべての z z で収束するときは収束半径は r=\infty r = ∞ と規定する。 a=0, x\in \mathbb {R} a = 0,x ∈ R とすると,最初の定義に一致しますね。 以降は,こちらの一般的な定義の方で進めていきます。 収束半径の求め方 さて,収束判定法の求め方として, ダランベールの公式による判定 コーシーアダマール公式の導き方や、体積計算の問題の解き方は、リンク先のページでご覧になれます。 お使いのブラウザでは JavaScript が無効になっています。 当サイトは数式表示に JavaScript を利用しているため、これを無効にしているとページが正しく表示されません。こうしてエラトステネスは地球の大きさを測ったのです.もちろんその値は近似的なものでしかありませんでした.現在知られている地球の半径は約 6360 kmです. (注)地球は太陽の周りを一年かけて一周します.その軌道面に対して地球の自転軸は 235




小3 円 円の半径と直径 日本語版 Youtube



収束半径の求め方を教えてください 画像の問題の解き方を教えてく Yahoo 知恵袋
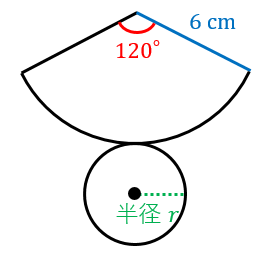
扇形の半径を求めるときも、面積の公式または弧の長さの公式を利用します。 度数法の場合扇形の半径 角度が度数法で与えられた場合、扇形の半径は次のように求められます。 扇形の半径の求め方(度数法) 中心角 の扇形の半径 は、 面積 がわかっている場合 より 弧の長さ がわかっている場合 より 例題はここをクリック 弧度法の場合扇形の半径 角度が弧度法で与えられ5年 学研教育情報資料センター 算数 学習相談 小/算数/5年/図形/ 正多角形と円/理解シート最小屈曲半径について ケーブルを屈曲する際には、ケーブルの損傷や性能の劣化に配慮する必要がある。 最小屈曲半径は表1,表2の通りとする。 (℃±10℃での最小屈曲半径)



円の方程式 公式




曲率半径の公式 材料力学曲げ編 第2講 Youtube
曲率半径の意味 意味:曲線の微小な一部分を 円弧とみなした ときその 円弧の半径 曲線 y = f(x) 上の点 A から曲線に沿って Δs だけ移動した点を B とする. Δs 部分を円弧とみなし,その円弧の中心を点 O ,角 AOB を Δα とする. このとき, 円の半径 R単位格子の一辺の長さと原子半径の関係は,原子が互いに接している面を見つけることが基本です。 それでは,面心立方格子と体心立方格子について考えてみましょう。 面心立方格子 単位格子の各面の対角線上で原子が接しているので,単位格子の この問題の解き方を教えてください。 数学 ‼️‼️‼️至急です‼️‼️‼️ 地学基礎(高校)です。 極半径を求める問題なのですが、 偏平率を求める式に分かる数字を埋めて計算したのですが、上手く答えがでません。 この問題の答えはcmからmmにしない
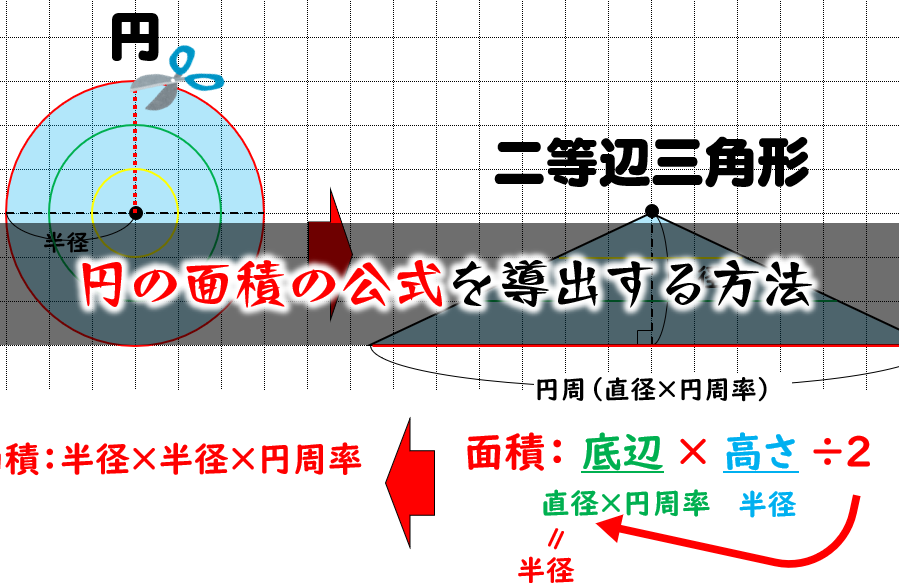



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく
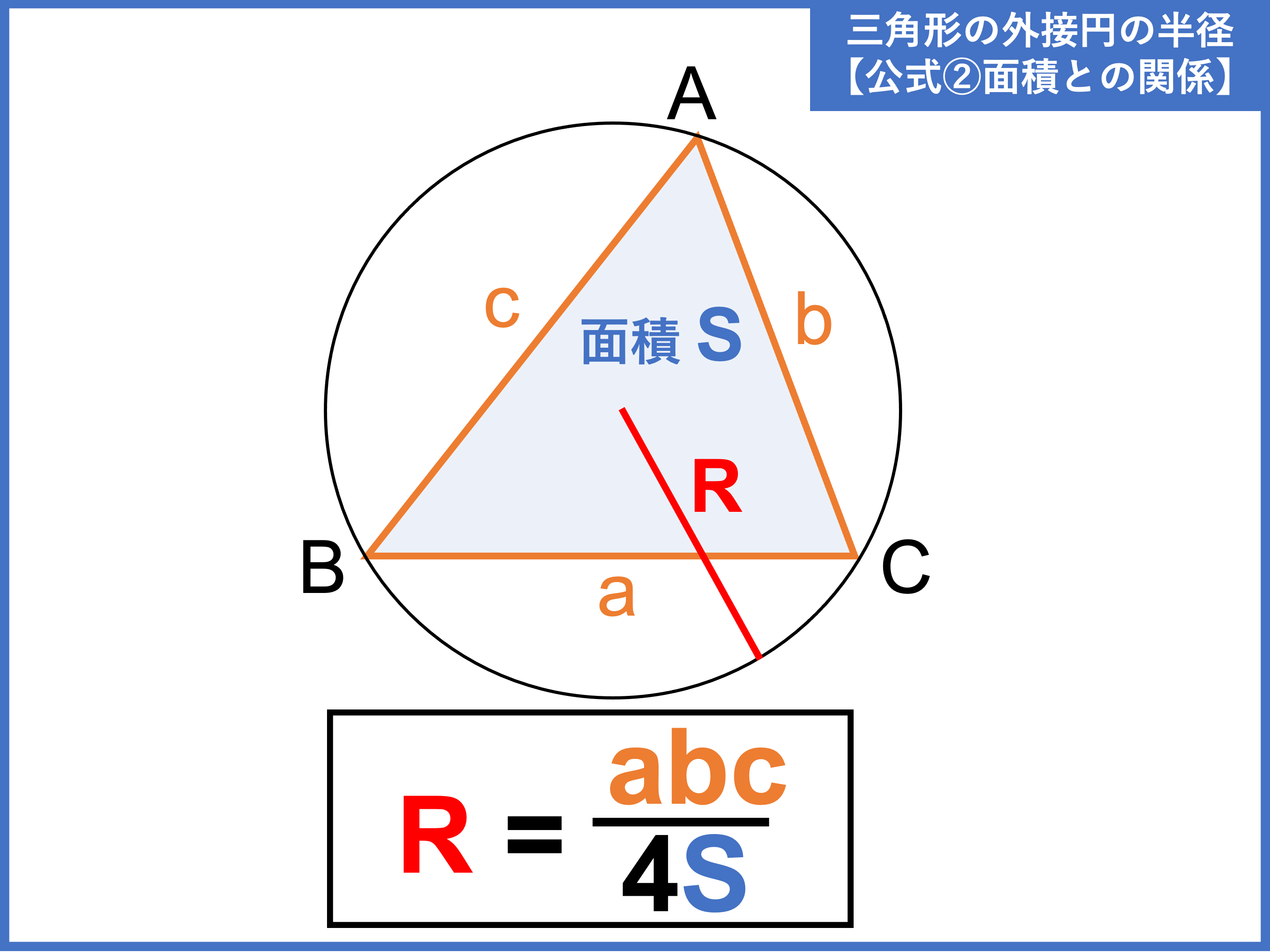
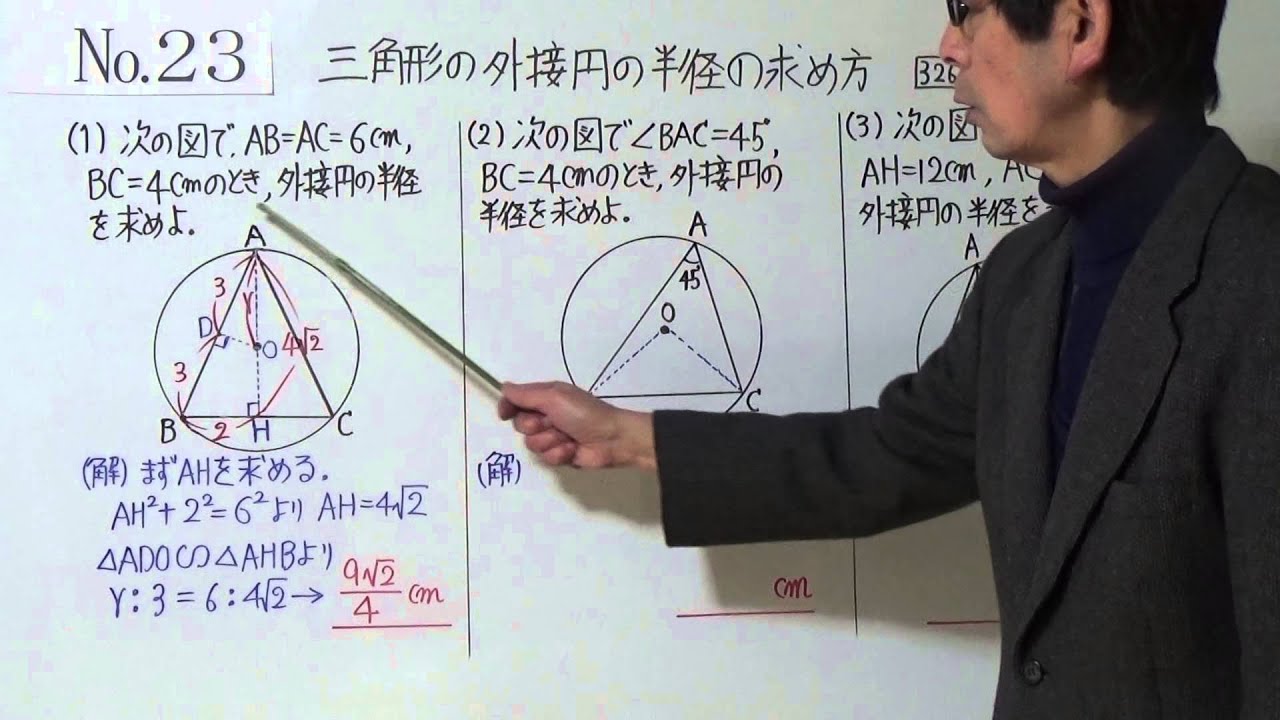
この計算機で出来ることは次の3つです。 直径・半径から、円の面積と円周の長さを求める。 円の面積から、直径・半径と円周の長さを求める。 円周の長さから、直径・半径と円の面積を求める。 計算には、javascriptライブラリ BigNumberjs を使用してい 三角形の外接円の半径の公式 公式① 正弦定理 公式② 3 辺と三角形の面積から求める 三角形の外接円の半径の求め方 ① 1 辺と向かい合う角がわかる場合 ② 3 辺の長さと面積がわかる場合 ③ 3 辺の長さだけがわかる場合 外接円の性質 性質① 外心と垂直二等分線 性質② 外心と各頂点との距離 外接円の計算問題 計算問題①「半径から角度を求める」 計算問題②「2 辺と1 角から半径を求める」 円の半径と弦長から矢高を求めたいときの計算式を教えて下さい。 できればエクセルに入力する時の数式も教えていただけると幸いです。 三角形の2辺の長さから残りの1辺の長さを求める求め方を教えてください。またそれをexcelのセルに入力する数式も



半径から円周の求め方は 1分でわかる計算式 半径1の円周の長さ 直径から円周の求め方 面積の求め方




扇形の弧の長さの求め方 公式と計算例
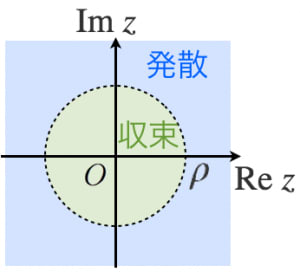



収束半径の意味と求め方 高校数学の美しい物語



円の面積の求め方を教えてください 4分の1の大きさの円 です Yahoo 知恵袋




3分で分かる 三角形の外接円の半径の長さの求め方をわかりやすく 合格サプリ




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




小6 算数 小6 旧 円の面積 Youtube



円の方程式の公式や求め方をわかりやすく解説 円の接線も 受験辞典




おうぎ形 半径の求め方をイチから解説 Youtube
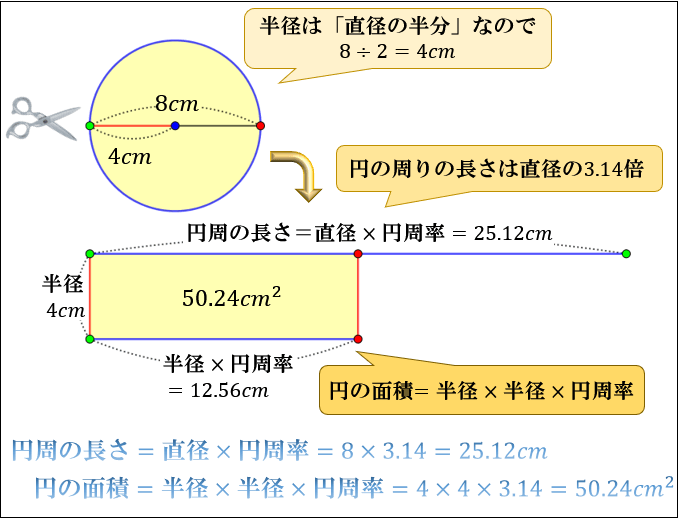



円周の求め方と円の面積について アタリマエ




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ
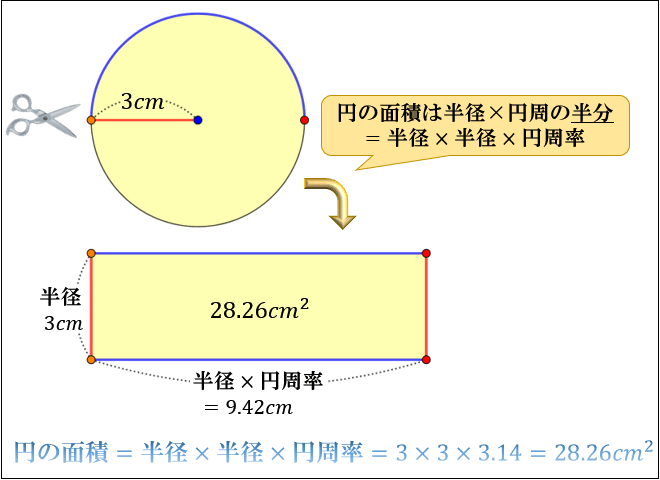



円周の求め方と円の面積について アタリマエ
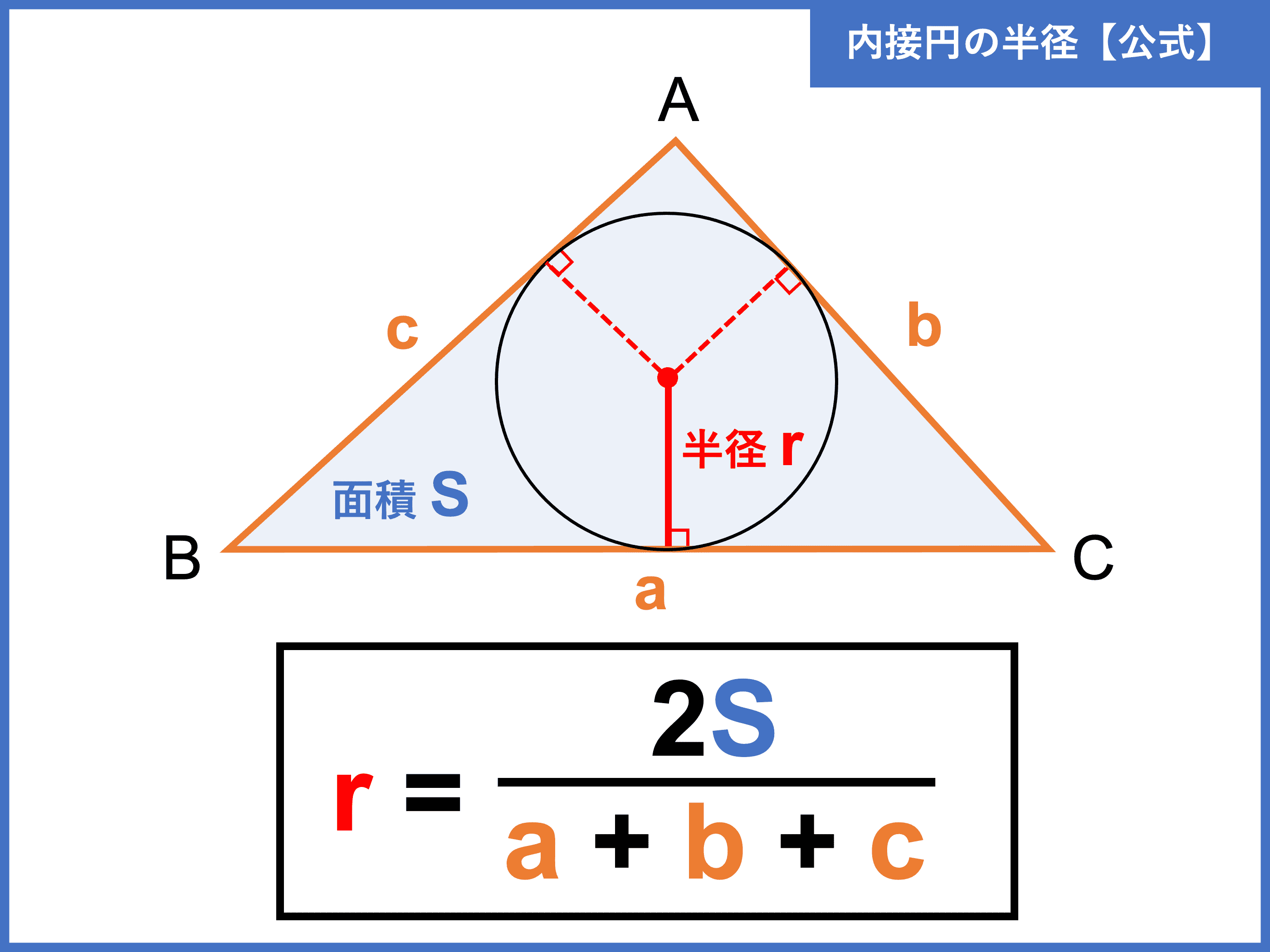



内接円とは 半径の公式や求め方 性質をわかりやすく解説 受験辞典




円周の求め方と円の面積について アタリマエ




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



円の方程式の導き方 数学 苦手解決q A 進研ゼミ高校講座




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学




扇形の半径の求め方 計算のやり方をイチから解説していくぞ 中学数学 理科の学習まとめサイト




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ



外接円とは 半径の公式や求め方 性質をわかりやすく解説 受験辞典




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ




円 扇形 の面積 周や弧の長さの公式 数学fun




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ



中3 23 4三角形の外接円の半径 Youtube



円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




File 面心立方格子の原子半径の求め方 Svg Wikimedia Commons




なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名



円の方程式と半径の関係は 1分でわかる意味と関係 求め方 公式と変形式
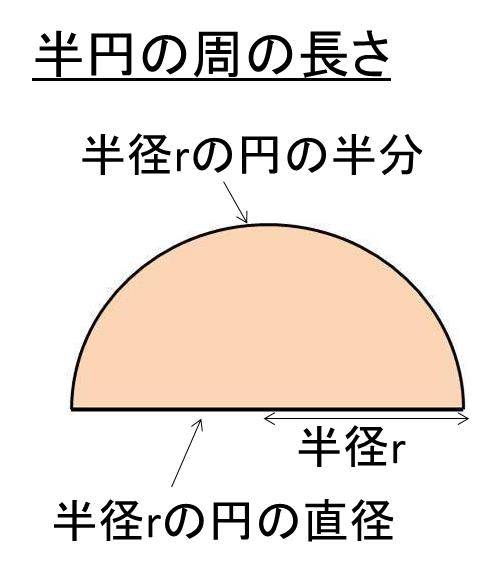



半円の周の長さの計算方法 白丸くん
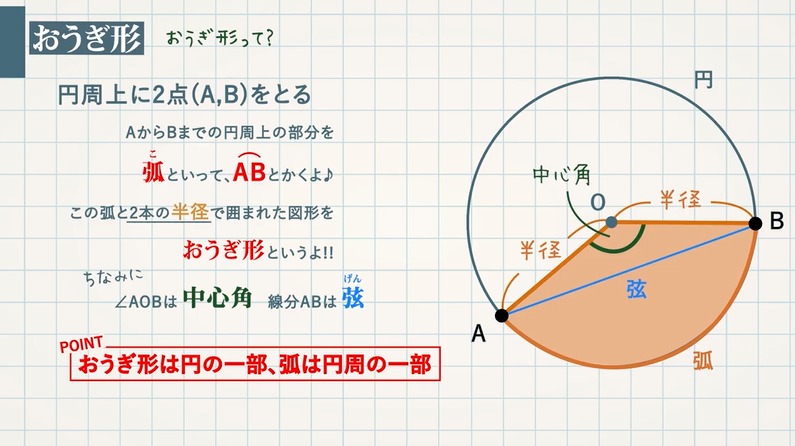



おうぎ形まとめ 弧と面積の求め方 教遊者
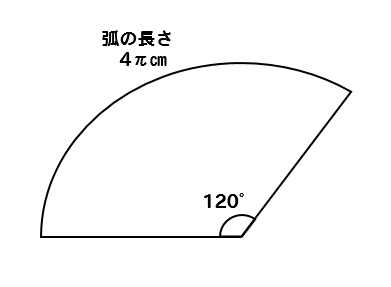



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
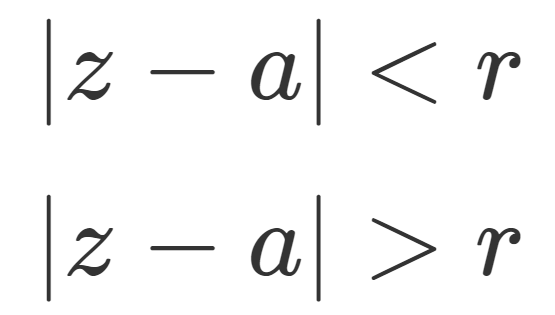



べき級数 収束半径の定義と求め方とその具体例3つ 数学の景色




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
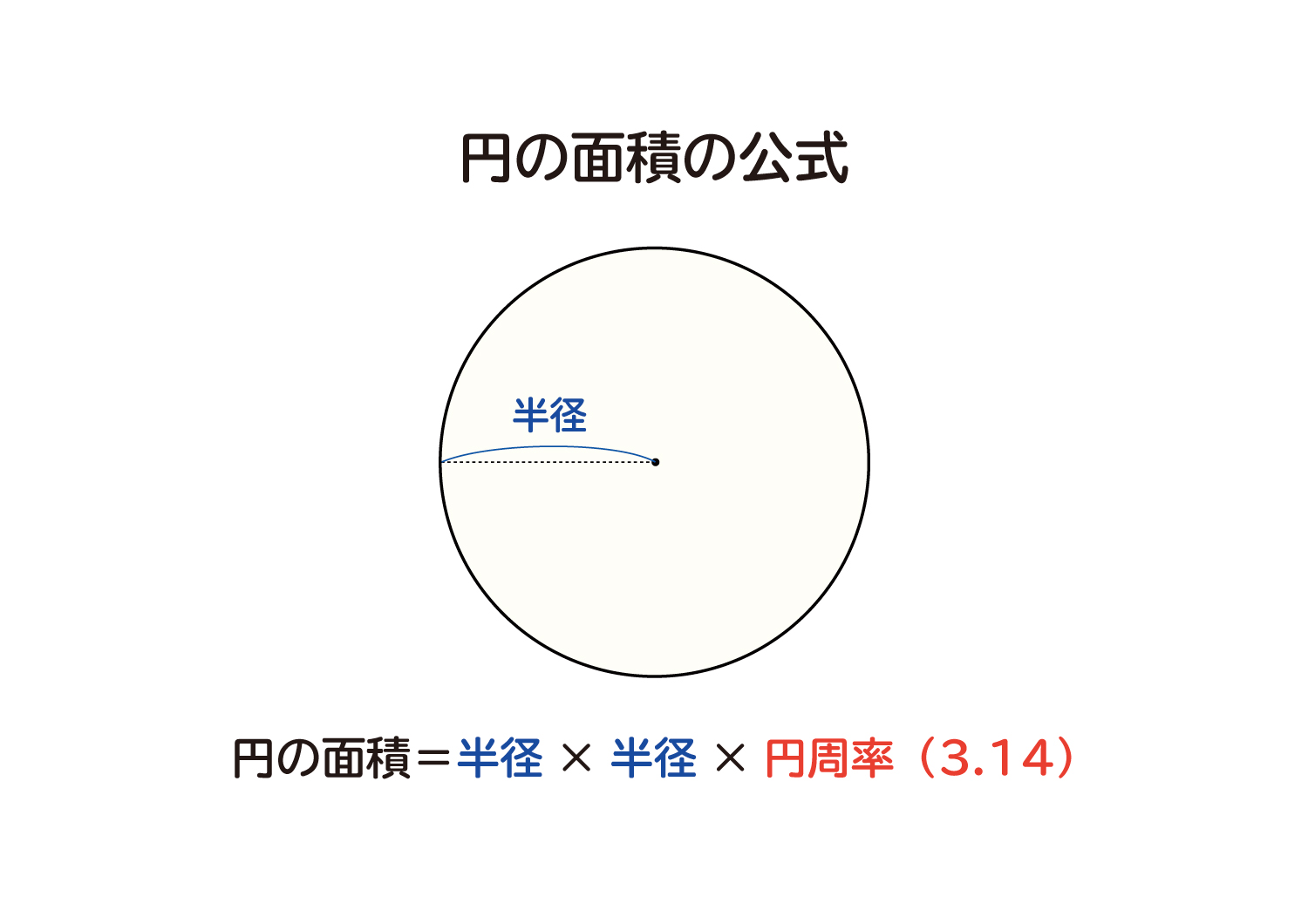



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル




円周の求め方 公式と計算例




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット



3




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく
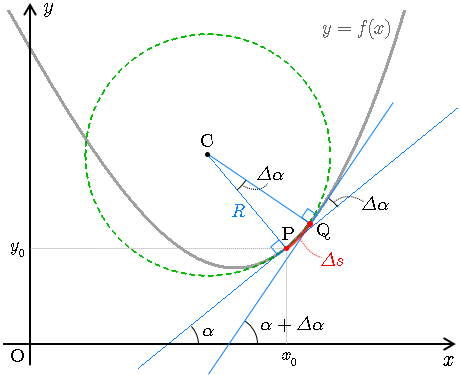



曲率半径




円周の求め方と円の面積について アタリマエ




円柱の表面積の求め方 公式と計算例




小学生でもできる円周率の求め方 いろいろな方法を紹介 数学の面白いこと 役に立つことをまとめたサイト




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




円の面積 円周の求め方 公式 小学生 中学生の勉強



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ



オンラインショップ セーフラン ドア路面標識ステッカー 半径10mm4分の1円扇形 黄 通販 2ebefd94 正規販売店 Aseraseo Com




円の面積の求め方 公式と計算例



2番の収束半径の求め方を教えて欲しいです ダランベール判定 Yahoo 知恵袋




おうぎ形 半径の求め方 数学の記録




円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ




外接円の半径の求め方 Menkarm World




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト
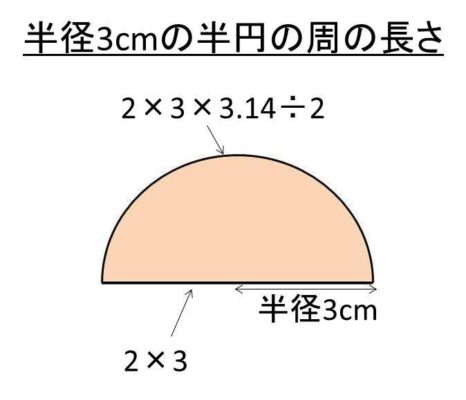



半円の周の長さの計算方法 白丸くん
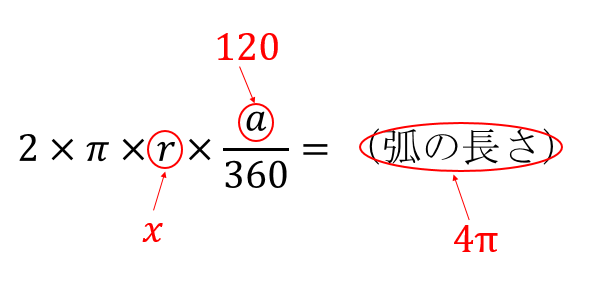



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




地球半径の測定 遥かなる 知 平線
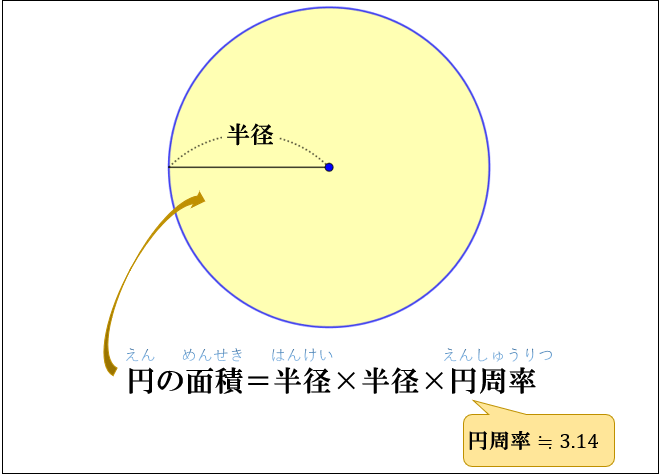



円周の求め方と円の面積について アタリマエ




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋
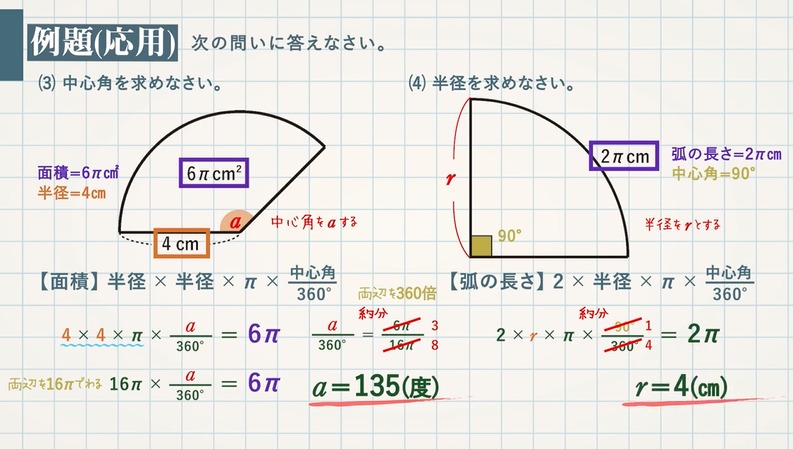



おうぎ形まとめ 弧と面積の求め方 教遊者




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
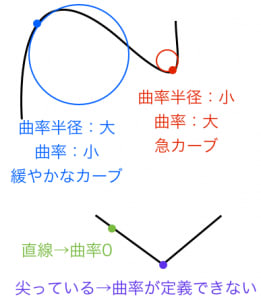



曲率 曲率半径の感覚的な意味と求め方 高校数学の美しい物語



円の面積の求め方




円の方程式の求め方まとめ パターン別に解説するよ 数スタ




公式 傍接円の半径を求める 立教新座 18 Youtube



球の体積の求め方 公式の覚え方を語呂合わせで覚えよう 中学数学 テラコヤプラス By Ameba
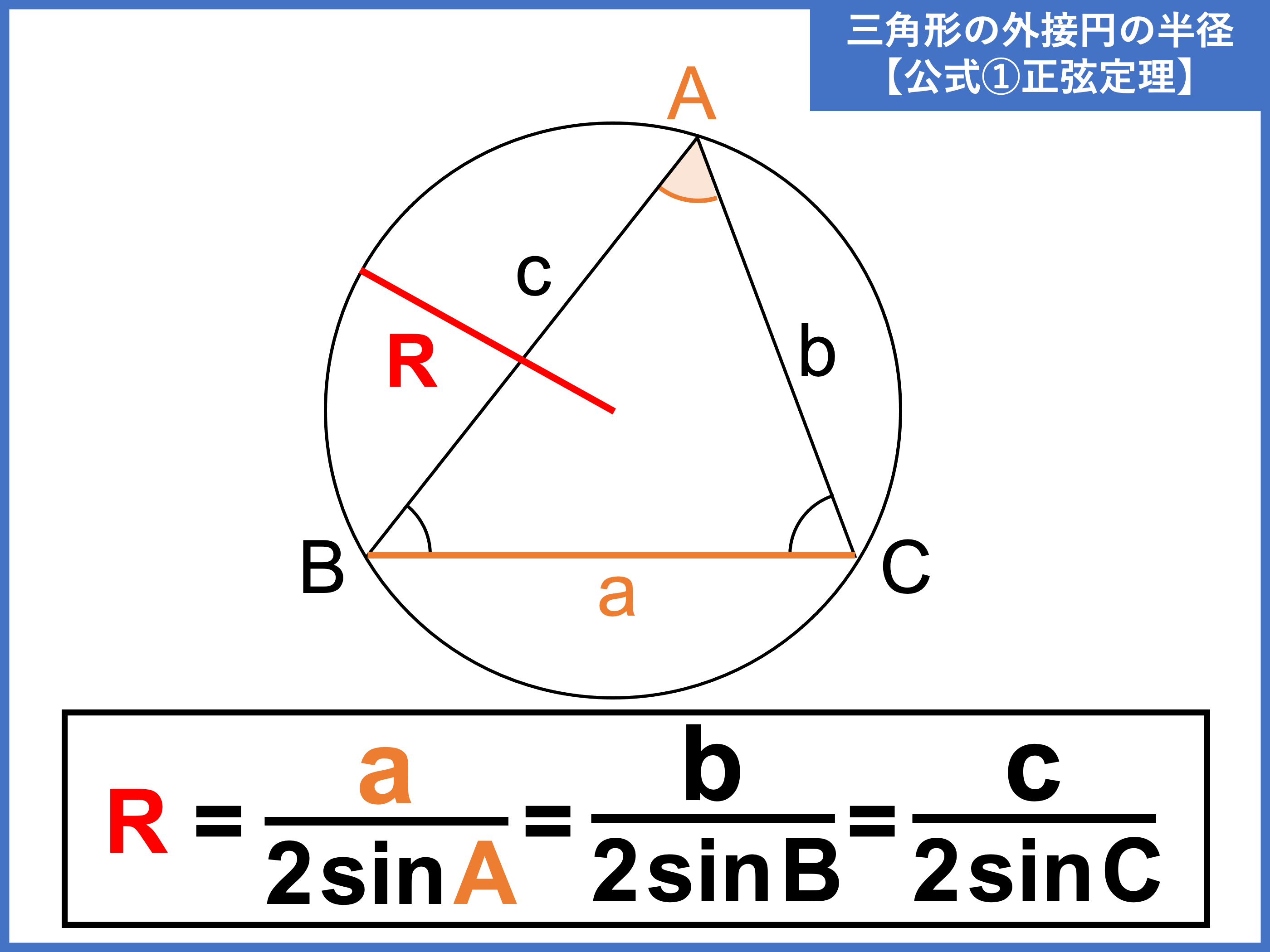



外接円とは 半径の公式や求め方 性質をわかりやすく解説 受験辞典
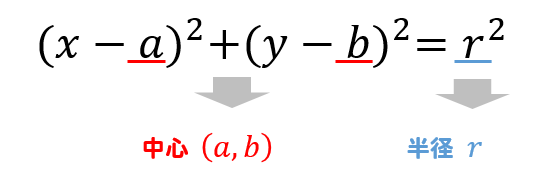



円の方程式 中心の座標と半径の求め方を解説 数スタ
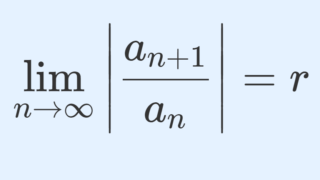



べき級数 収束半径の定義と求め方とその具体例3つ 数学の景色



小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ
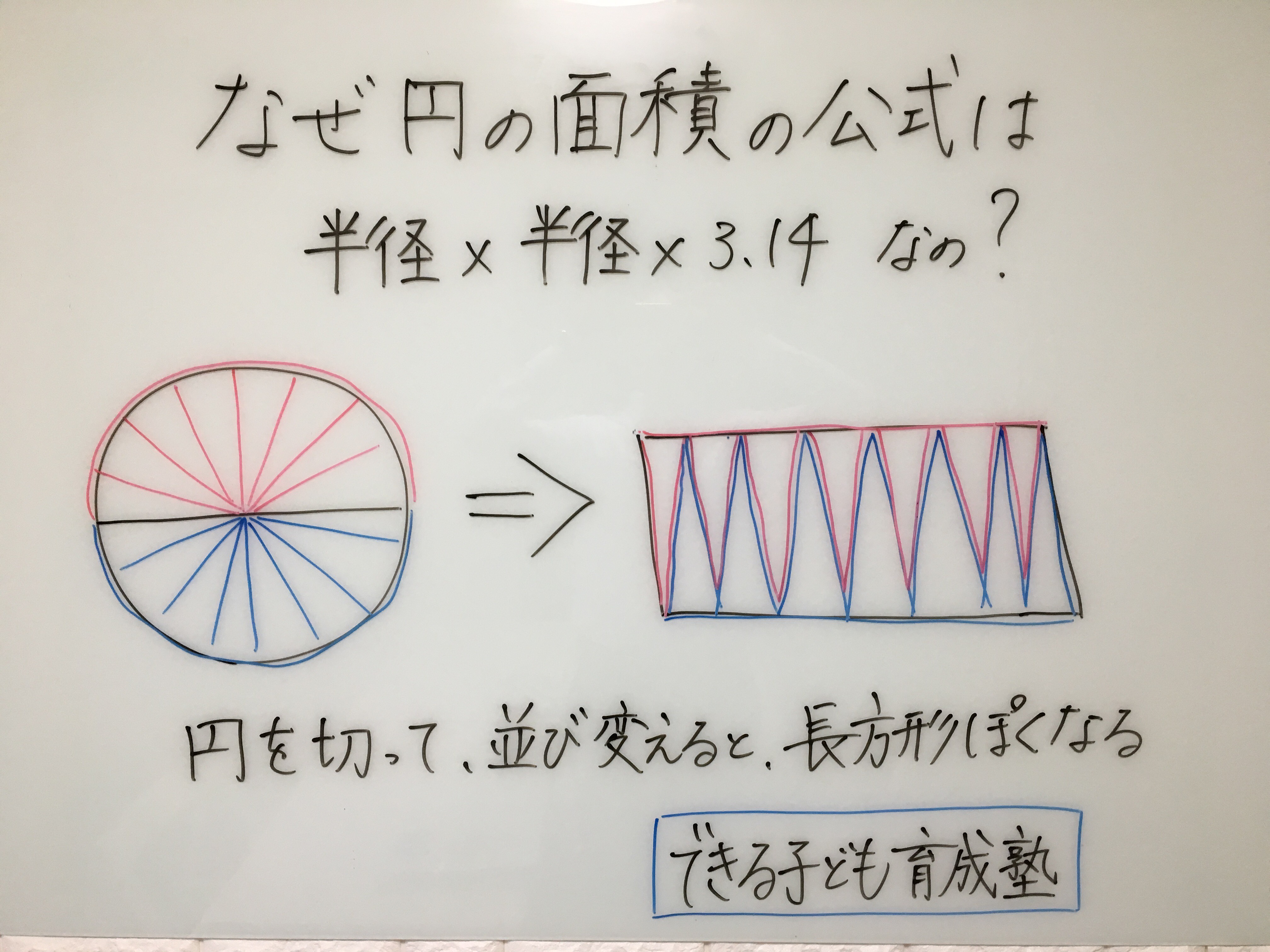



円の面積の求め方 公式 の理由を小学生に教える方法




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿